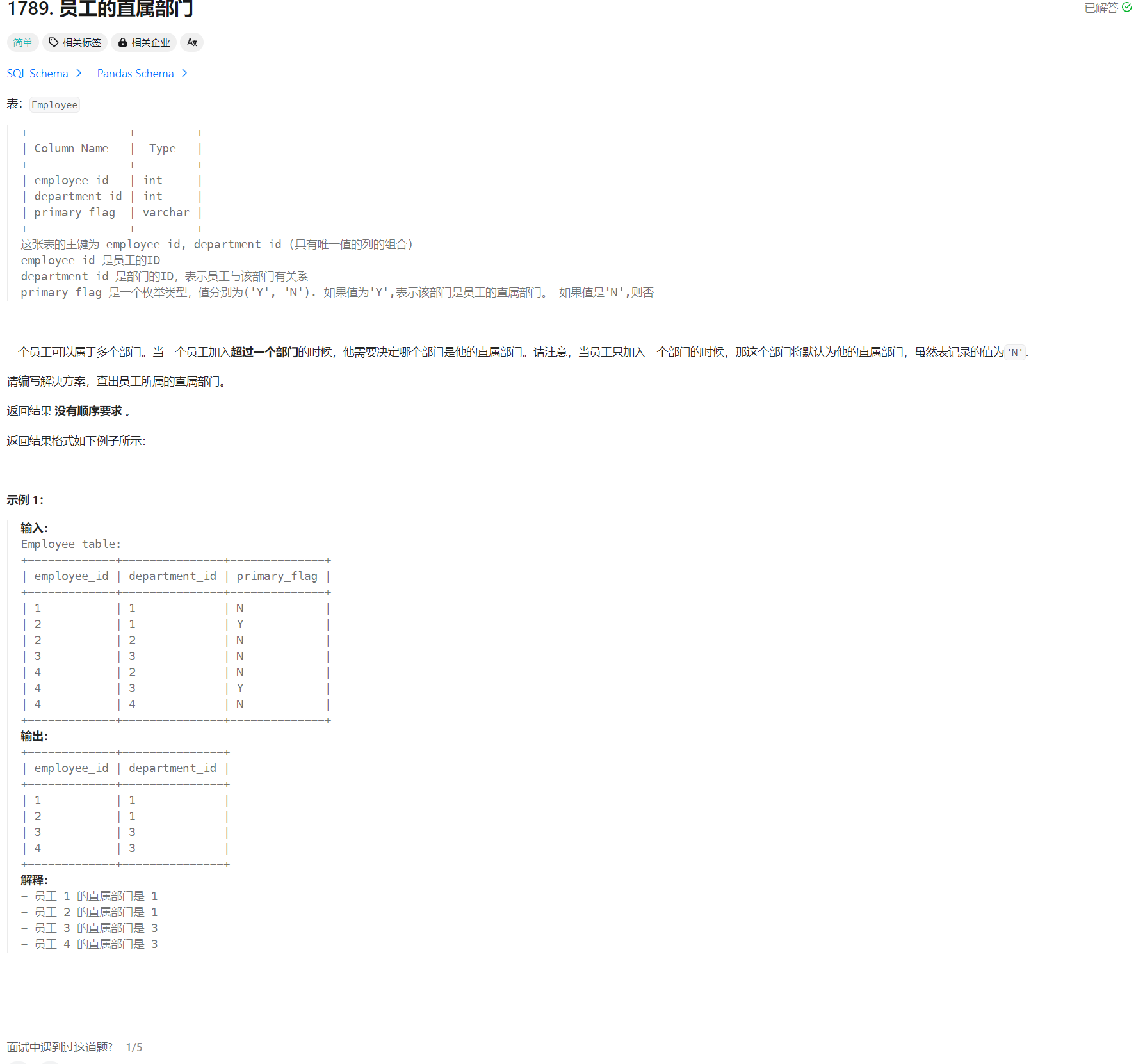
目录
- 题目
- 1- 思路
- 2- 实现
- ⭐300. 最长递增子序列——题解思路
- 3- ACM 实现
题目
- 原题连接:300. 最长递增子序列
1- 思路
- 模式识别:最长递增子序列——> 利用动规五部曲 解决 ——> 借助 i 和 j 指针,其中 j < i
动规五部曲
- 1.定义 dp 数组确定 dp数组的含义
int[] dp = new int[nums.length]:——> dp[i] 代表 以 i 为结尾的数组的最长递增子序列
- 2.递推公式
if(nums[i]>nums[j]) { dp[i] = Math.max(dp[i],dp[j]+1); }
- 3.初始化
- 所有初始化都为 1 ,
Arrays.fill(dp,1);
- 所有初始化都为 1 ,
- 4.遍历顺序
- 利用
i和j进行遍历
- 利用
2- 实现
⭐300. 最长递增子序列——题解思路

class Solution {
public int lengthOfLIS(int[] nums) {
// 1. 定义 dp数组
int[] dp = new int[nums.length];
// 2. 递推公式
// if(nums[i] > nums[j] )
// {dp[i] = Math.max(dp[i],dp[j+1]);}
// 3. 初始化
Arrays.fill(dp,1);
// 4. 遍历顺序
for(int i = 1 ; i < nums.length;i++){
for(int j = 0 ; j < i ;j++){
if(nums[i]>nums[j]){
dp[i] = Math.max(dp[i],dp[j]+1);
}
}
}
int res = 1;
for(int i:dp){
res = Math.max(res,i);
}
return res;
}
}
3- ACM 实现
public class longetSub {
public static int longest(int[] nums) {
// 1.定义 dp 数组
int[] dp = new int[nums.length];
// 2. 递推公式
// dp[i] = Math.max(dp[i],dp[j]+1);
// 3. 初始化
Arrays.fill(dp, 1);
// 4.遍历顺序
for (int i = 1; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int res = 1;
for (int i : dp) {
res = Math.max(i,res);
}
return res;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("输入数组长度");
int n = sc.nextInt();
int[] nums = new int[n];
for(int i = 0 ; i < n ; i ++){
nums[i] = sc.nextInt();
}
System.out.println("最长递增子序列为"+longest(nums));
}
}